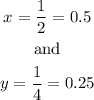We have the following 2x2 system of equations:
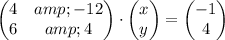
and we need the vector solution
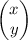
Then, we need to find the inverse matrix of the 2x2 matrix on the left hand side. For any 2x2 matrix A,
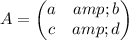
the inverse is given as.
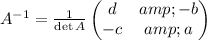
where detA denotes the determinant. Therefore, by means of the inverse matrix, the general solution for any 2x2 matrix will be
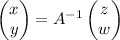
for any vector with entries z and w.
In our case, the determinat is
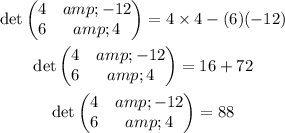
Therefore, the solution of our system will be
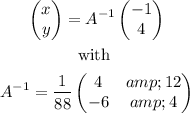
Explicitly,
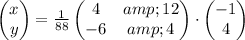
Now, lets make the product of the right hand side. It yields,
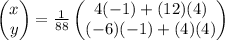
which gives
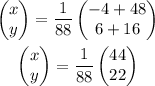
since 22x4=48 and 44x2=88, we have
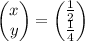
Therefore, the solution of the system is