Given:
given points are X(-2,5) and Y(2,-3).
Find:
we have to find the coordinates of the point P on directed line segment XY that partitions the segment XY in such a way that the ratio of XP:PY = 4:1.
Step-by-step explanation:
we will use section formula to find the coordinates of point P,
If a line XY is divided into two sections in the ratio m:n, then the x and y coordinates of point P are
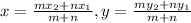
here, m = 4 and n = 1 and the points x1= -2, x2 = 2, y1 = 5 and y2= -3.
Therefore, the coordinates of point P are
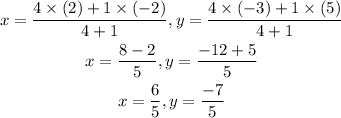
Therefore, the coordinates of point P are
