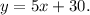Question

Find an equation for the line with the given properties. Express your answer using either the general form or the slope-intercept form of the equation of a line.Parallel to the line y=5x containing the points (-5,5)

Answer 1

To answer this question we will use the following slope-point formula for the equation of a line:

`y-y_1=m(x-x_1)\text{.}`

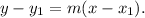
Recall that two lines are parallel if they have the same slope.

Now, notice that the given equation is y=5x, therefore, the slope of the given equation is 5.

Using the slope-point formula, we get that the equation of the parallel line to y=5x that passes through (-5,5) is:

`y-5=5(x-(-5))\text{.}`

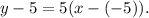
Simplifying the above equation we get:

`\begin{gathered} y-5=5(x+5), \\ y-5=5x+25. \end{gathered}`

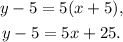
Adding 5 to the above equation we get:

`\begin{gathered} y-5+5=5x+25+5, \\ y=5x+30. \end{gathered}`

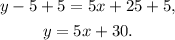
Answer:

`y=5x+30.`