Question

it said my answer is wrongTwo cards are selected from a standard deck of 52 cards. The first card is not replaced before the second card selected. Find the probability of selecting a two and then selectinga a king

Answer 1

To answer this question, we need to have into account the following:

1. We have a standard deck of cards of 52 cards.

2. The first card is not replaced before the second card is selected.

3. We have four cards denominated "2" in a standard deck of cards.

4. We also have four cards denominated "king" in a standard deck of cards.

Now, the probability of selecting a two from the standard deck of cards is:

`P(X=2)=(4)/(52)=(1)/(13)\Rightarrow P(X=2)=(1)/(13)`

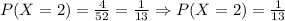
Since the first card is not replaced (it did not return to the deck of cards), we now have 51 cards. Now, the probability of selecting a king is:

`P(X=K)=(4)/(51)`

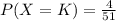
Then, the probability of these two events is:

`P=(1)/(13)\cdot(4)/(51)\Rightarrow P=(4)/(663)=0.00603318250377\approx0.006`

If we round to three decimals the probability is, approximately, P = 0.006.