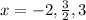Question

If f(x)=2x^3-5x^2-9x+18 and x+2 is a factor of f(x), then find all of the zeros of f(x) algebraically.

Answer 1

Given the expression below

`f(x)=2x^3-5x^2-9x+18`

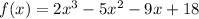
And x + 2 is a factor

Applying long division

`(2x^3-5x^2-9x+18)/(x+2)`

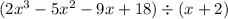
After the long divison, factorizing the quotient gives,

`\begin{gathered} 2x^2-9x+9 \\ =2x^2-6x-3x+9 \\ =2x(x-3)-3(x-3) \\ =(2x-3)(x-3) \end{gathered}`

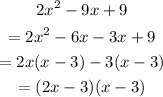
The factored form of the expression is

`f(x)=(x+2)(2x-3)(x-3)_{}`

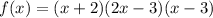
To find the zeros, equating each factor to zero, i.e

`\begin{gathered} (x+2)(2x-3)(x-3)_{}=0 \\ x+2=0 \\ x=-2 \\ 2x-3=0 \\ 2x=3 \\ (2x)/(2)=(3)/(2) \\ x=(3)/(2) \\ x-3=0 \\ x=3 \\ x=-2,(3)/(2),3 \end{gathered}`

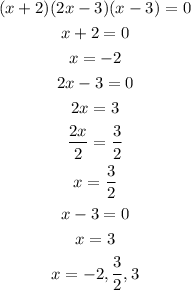
Hence, the zeros of f(x) are

`x=-2,(3)/(2),3`