We are given that Bharat travels with a speed of 12 km/h and Ingrid travels at a speed of 14 km/h.
Part a. Given that the distance that Bharat has traveled is "b" this means that the distance that Ingrid has traveled is:
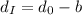
Where:
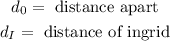
We can see this in the following diagram:
Part b. We need to determine two equations to solve for the time when the distance apart is 78 kilometers. To do that we need to remember that distance is the product of velocity and time. Therefore, if the distance of Bharat is "b", then the first equation is:
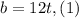
Now, if "I" is the distance of Ingrid, then the second equation is
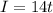
But, we already know the distance that Ingrid has traveled, therefore, we can substitute:
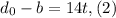
Part 3. Now, we are asked to determine the time. To do that we will add both equations:
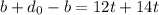
Now we can cancel out the "b":
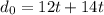
Adding like terms:
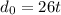
Since the distance apart is 78 kilometers, we can substitute:
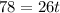
Now we divide both sides by 26;
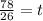
solving we get:
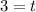
Therefore, after 3 seconds they will be 78 km apart.