Question

The vertices of quadrilateral LMNP are L (-1,7) M(4,9) N(8,-1) P(3,-3)

Answer 1

First, let's write the distance formula:

`d\text{ = }\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Probably we should draw the points to get an image of what we have:

Then, we can calculate the distance between each point, so that we find out if all the sides are equal or different.

`\begin{gathered} LM\text{ =}\sqrt[\square]{(4-(-1))^2+(9-7)^2} \\ LM\text{ = }\sqrt[\square]{29} \\ MN=\sqrt[\square]{(8-4)^2+(-1-9)^2} \\ MN=2\sqrt[\square]{29} \\ NP=\sqrt[\square]{(3-8)^2+(-3-(-1))^2} \\ NP=\sqrt[\square]{29} \\ PL=\sqrt[\square]{(-1-3)^2+(7-(-3))^2} \\ PL=2\sqrt[\square]{29} \end{gathered}`

Since we have 2 pairs of sides with the same dimension, then we assume that it is a rectangle or a paralelogram.

We can get the slope of two lines in order to know if they are perpendicular or they have certain angle between each other.

`\begin{gathered} m_(LM)=(9-7)/(4-(-1))=(2)/(5) \\ m_(PL)=(-3-7)/(3-(-1))=(-10)/(4)=-(5)/(2) \end{gathered}`

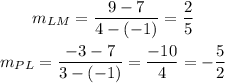
Since the slopes are reciprocal and have different sign, we asure that both lines are perpendicular, therefore, we are talking about a rectangle.