Question

The number of salespeople assigned to work during a shift is apportioned based on the average number ofcustomers during that shift. Apportion 19 salespeople using Hamilton's method given the informationbelow.ShiftMorning Midday Afternoon EveningAverage number of customers 105450475Salespeople to assign300

Answer 1

The number of salespeople to be assigned to each shift is;

`\begin{gathered} \text{Morning }=2 \\ \text{Midday }=4 \\ \text{Afternoon }=6 \\ \text{Evening }=7 \end{gathered}`

Step-by-step explanation:

Using Hamilton's method.

let d represent the divisor.

`d=\frac{\text{ total average number of customers for the day}}{\text{number of salespeople to be apportioned}}`

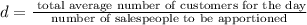
total average number of customers for the day is the sum of all the average given;

`105+300+450+475=1330`

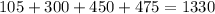
The total number of salespeople to be apportioned is given as 19.

the divisor d is;

`\begin{gathered} d=(1330)/(19)=70 \\ d=70 \end{gathered}`

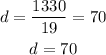
To determine number of salespeople N to assign to each shift, we will divide the average number A of customers in that shift by the divisor d.

for morning;

A=105

`\begin{gathered} N=(A)/(d)=(105)/(70) \\ N=1.5 \end{gathered}`

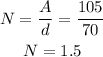
for midday;

A=300

`\begin{gathered} N=(300)/(70) \\ N=4.29 \end{gathered}`

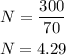
for afternoon;

A=450

`N=(450)/(70)=6.43`

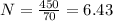
for Evening;

A=475

`\begin{gathered} N=(475)/(70) \\ N=6.79 \end{gathered}`

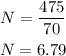
To get an exact whole number let us round each up to the nearest whole number.

The final answer is;

`\begin{gathered} \text{Morning }=2 \\ \text{Midday }=4 \\ \text{Afternoon }=6 \\ \text{Evening }=7 \end{gathered}`