Question

Write a system of equations to describe the situation below, solve using substitution, and fill in the blanks.A pair of kids and a pair of adults decided to compete in a three-legged race. The kids got to start 9 yards ahead of the adults, since they had shorter legs. When they were told to start, the kids hobbled forward at a rate of 2 yards per second, and the adults hobbled after them at a rate of 3 yards per second. Soon they were side-by-side. How long did that take? How far did the adults go?

Answer 1

27 yards

9 seconds

Explanation:

With the help of the statement, we can establish an equation for children and an equation for adults. If x is the race time, the equations would look like this:

`\begin{gathered} k=9+2x \\ a=3x \end{gathered}`

If the distance traveled by kids is the same as for adults, we are left with the following:

`\begin{gathered} 9+2x=3x \\ \text{ solving for x:} \\ 3x-2x=9 \\ x=9 \end{gathered}`

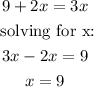
Now, we calculate the distance like this:

`\begin{gathered} a=9\cdot3 \\ a=27\text{ yards} \end{gathered}`

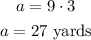
Therefore, the adults took 9 seconds and traveled 27 yards.