According to the image, the cue ball after the collision has a speed of 0.8 m/s with a direction of 20°. Let's use the rectangular components formulas to find each component.
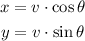
Where v = 0.8 m/s and theta = 20°.
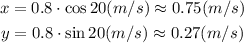
Now, we use the components to write the velocity of the cue ball, which is a vector

On the other hand, we can observe that the eight ball is still before the collision. To find its speed after the collision, we use the law of conservation of momentum.
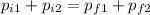
Where p = mv. Let's use all the given magnitudes.
![0.6\operatorname{kg}\cdot2m/s+0.6\operatorname{kg}\cdot0m/s=0.6\operatorname{kg}\cdot0.8m/s+0.6\operatorname{kg}\cdot v_(f2)]()
Then, we solve for the speed 2 (eight ball speed):
![\begin{gathered} v_(f2)=\frac{1.2kg\cdot m/s-0.48kg\cdot m/s}{0.6\operatorname{kg}} \\ v_(f2)=\frac{0.72\operatorname{kg}\cdot m/s}{0.6\operatorname{kg}} \\ v_(f2)=1.2m/s \end{gathered}]()
The final speed of the eight ball is 1.2 m/s. But we have to find the angle of the eight ball after the collision in order to find its components. To find the angle, we just have to subtract 90°-20° = 70°.
Now, we can find the rectangular components.
![\begin{gathered} x=v\cdot\cos \theta \\ y=v\cdot\sin \theta \end{gathered}]()
Where v = 1.2 m/s and theta = 70°.
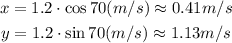
The x-component of the velocity of the eight ball is 0.41i (m/s) and the y-component of the velocity of the eight ball is 1.13j (m/s).
The eight ball travels at a 70° angle after the collision.
The magnitude of the eight ball's velocity after the collision is 1.2 m/s.