Lets draw a picture of our points:
since triangles are similar the following ratios must be preserved:
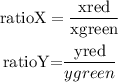
where these values come from the following picture:
for the first x red-ratio, we have
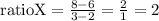
for green-ratio, we have
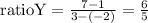
Then, by applying these results, the ratios from point S=(x,y) to point N=(7,5) must be
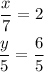
From the first relation, we get

and from the second relation, we have
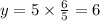
then, the searched point S has coordinates S=( 14,6)