Question

By what percentage does the drag force on a car increase as it goes from 61 km/h to 113 km/h?

Answer 1

Given,

The initial speed of the car, u=61 km/h

The final speed of the car, v=113 km/h

The drag force on an object is given by,

`F=(1)/(2)\rho v^2C_DA`

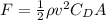
Where:

• ρ is the density of the air.

,

• v is the speed of the object.

,

• C_D is the drag coefficient.

,

• A is the area of cross-section of the object.

In the given problem, only the speed of the car changes. And density of the air, drag coefficient, and area of the cross section remains the same.

Thus, the initial drag force on the car is

`F_i=(1)/(2)\rho u^2C_DA`

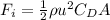
The final drag force is given by,

`F_f=(1)/(2)\rho v^2C_DA`

The percentage increase in the drag force is given by,

`P=(F_f-F_i)/(F_i)_{}*100`

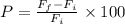
On substituting,

`\begin{gathered} P=((1)/(2)\rho v^2C_DA-(1)/(2)\rho u^2C_DA)/((1)/(2)\rho u^2C_DA)*100 \\ =((1)/(2)\rho C_DA(v^2-u^2))/((1)/(2)\rho u^2C_DA)*100 \\ =(v^2-u^2)/(u^2)*100 \end{gathered}`

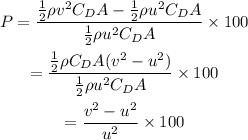
On substituting the values of v and u,

`\begin{gathered} P=(113^2-61^2)/(61^2)*100 \\ =243\% \end{gathered}`

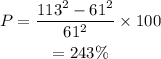
Thus, the percentage increase in the drag force is 243%