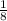Question

there is a stack of 8 cardseach given a different number from 1-8suppose we select a card from the stack, Replace it, and then Randomly select another card.what is the Probability that the 1st card is an Odd num and the 2nd card is Greater than 6?

Answer 1

The probability of a particular event A occurring from an experiment is obtained from the number of ways that A can occur divided by the total number of possible outcomes. That is;

`\begin{gathered} P(A)=(n(A))/(n(T)) \\ \text{Where;} \\ P(A)=\text{ probability of event A} \\ n(A)=\text{ number of possible ways event A can occur} \\ n(T)=\text{ total number of possible outcomes} \end{gathered}`

In a stack of 8 cards with different numbers;

The probability that the first card is an odd number and the second card is greater than 6 is the product of the probability of odd number and the probability of greater than 6. That is;

`P(\text{Odd and greater than 6)}=P(odd)* P(greater\text{ than 6)}`

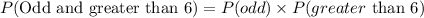
We have;

`\begin{gathered} P(\text{odd)}=\frac{n(\text{odd)}}{n(T)} \\ P(\text{odd)}=(4)/(8) \\ P(\text{odd)}=(1)/(2) \end{gathered}`

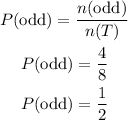
Also,

`\begin{gathered} P(\text{greater than 6)=}\frac{\text{n(greater than 6)}}{n(T)} \\ P(\text{greater than 6)=}\frac{\text{2}}{8} \\ P(\text{greater than 6)=}(1)/(4) \end{gathered}`

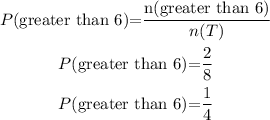
So, the probability that the first card is an odd number and the second is greater than 6 is;

`\begin{gathered} P(\text{Odd and greater than 6)}=(1)/(2)*(1)/(4) \\ P(\text{Odd and greater than 6)}=(1)/(8) \end{gathered}`

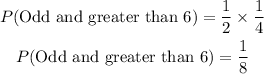
FINAL ANSWER:

`(1)/(8)`