Question 2.
Given:
• QR = 5
,
• PT = 4
Let's find the perimeter of the quadilateral PQRS.
Here, the radius of the circle is 5 units.
Thus, we have:
TR = 5
RS = 5
PR = PT + TR = 4 + 5 = 9
Now, apply the tangent - radius theorem which states that the angle between a tangent a radius is a right angle.
To find the lengths of PQ and QS, apply Pythagorean Theorem:
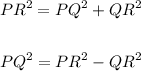
Where:
PR = 9
QR = 5
Thus, we have:
![\begin{gathered} PQ^2=9^2-5^2 \\ \\ PQ^2=81-25 \\ \\ PQ^2=56 \\ \\ PQ=\sqrt[]{56} \\ \\ PQ=\sqrt[]{14*4} \\ \\ PQ=\sqrt[]{14*2^2} \\ \\ PQ=2\sqrt[]{14} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/fetun35qx5t17zarcthi.png)
Now, using the two tangents theorem which states that two tangents whcih meet at the same point are equal in length.
We have:
PQ = PS = 2√14
To find the perimeter of quadilateral PQRS, apply the formula:
Perimeter = QR + RS + PQ + PS
Input the values and evaluate:
![\begin{gathered} \text{Perimeter}=5+5+(2\sqrt[]{14})+(2\sqrt[]{14}) \\ \\ \text{Perimeter}=10+4\sqrt[]{14} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/1ry9eiackvr0ito5xiqy.png)
Therefore, the perimeter of the quadilatral is:
![10+4\sqrt[]{14}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/okdrxw8ivhmgor0vd14i.png)
ANSWER: B
![10+4\sqrt[]{14}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/okdrxw8ivhmgor0vd14i.png)