Final answer:
The value of this integral depends on the specific form of the impulse response
 obtained from the inverse Fourier transform of the given frequency response
obtained from the inverse Fourier transform of the given frequency response
 . To find the exact value, you'll need to calculate the inverse Fourier transform and evaluate the resulting expression for
. To find the exact value, you'll need to calculate the inverse Fourier transform and evaluate the resulting expression for
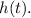
![\[ \int_(-\infty)^(\infty) h(t) dt \]](https://img.qammunity.org/2024/formulas/physics/college/50bkjk7gddfcxxe6rbc3goskj13wzo79dg.png)
Step-by-step explanation:
The question asks for the integral over all time of the impulse response of a linear time-invariant (LTI) system whose frequency response is given by H(ω) = 1 + ω² : 2. To find this integral, which is representatively ∫−∞⁺∞ h(t)dt, we can use the fact that the integral of the impulse response of an LTI system over all time is equal to the system's frequency response evaluated at ω = 0. From the given frequency response, H(ω) = 1 + ω² : 2, we can see that H(0) = 1. Therefore, the integral of the impulse response h(t) over all time is 1.
The impulse response of a system, denoted as
 , is related to the system's frequency response
, is related to the system's frequency response
 through the inverse Fourier transform. Specifically, the impulse response
through the inverse Fourier transform. Specifically, the impulse response
 is the inverse Fourier transform of the frequency response
is the inverse Fourier transform of the frequency response
 .
.
The inverse Fourier transform is given by:
![\[ h(t) = (1)/(2\pi) \int_(-\infty)^(\infty) H(\omega) e^(j\omega t) d\omega \]](https://img.qammunity.org/2024/formulas/physics/college/tpw93eugx1j91esvbs99kvygi8ttr1wpmz.png)
Given that
 , let's find the inverse Fourier transform
, let's find the inverse Fourier transform
![\(h(t)\):\[ h(t) = (1)/(2\pi) \int_(-\infty)^(\infty) \left(1 + (\omega^2)/(2)\right) e^(j\omega t) d\omega \]](https://img.qammunity.org/2024/formulas/physics/college/5hdtqymgpi459dbtq628mpx1rehzio3y5n.png)
Now, integrate this expression to find \(h(t)\). After finding \(h(t)\), you can then evaluate the integral:
![\[ \int_(-\infty)^(\infty) h(t) dt \]](https://img.qammunity.org/2024/formulas/physics/college/50bkjk7gddfcxxe6rbc3goskj13wzo79dg.png)
This integral represents the total area under the impulse response
 curve. The result of this integral will depend on the specific form of
curve. The result of this integral will depend on the specific form of
 obtained from the inverse Fourier transform.
obtained from the inverse Fourier transform.