Question

4. Object A has a mass of 10 kg and is moving at 5 m/s. Object B has a mass of 8 kg and is moving at 2 m/s. They then collide, and object B continues moving with a velocity of 4 m/s after the collision.a. What is the total initial momentum of object A and B?b. What should be the total final momentum of object A and B?c. What is the final velocity of object A?

Answer 1

a. 66 kg m/s

b. 66 kg m/s

c. 3.4 m/s

Step-by-step explanation:

Part a.

The total initial momentum of objects A and B is calculated as

`p_i=m_Av_(Ai)+m_Bv_(Bi)`

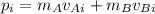
Where m is the mass and v is the initial velocity for each object. Replacing the values, we get:

`\begin{gathered} m_A=10kg \\ v_(Ai)=5\text{ m/s} \\ m_B=8kg \\ v_(Bi)=2m/s_{} \\ p_i=(10kg)(5m/s)+(8kg)(2m/s) \\ p_i=50kg\text{ m/s + 16 }kg\text{ m/s} \\ p_i=66kg\text{ m/s} \end{gathered}`

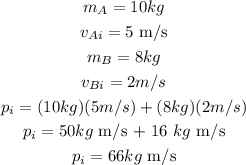
Therefore, the total initial momentum of objects A and B is 66 kg m/s

Part b.

By the conservation of momentum, the total final momentum is equal to the total initial momentum, so

`\begin{gathered} p_f=p_i \\ p_f=66kg\text{ m/s} \end{gathered}`

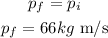
Therefore, the total final momentum of objects A and B is 66 kg m/s.

Part c.

The final momentum is also equal to:

`p_f=m_Av_(fA)+m_Bv_(fB)`

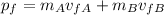
Solving for the final velocity of object A, we get:

`\begin{gathered} p_f-m_Bv_(Bf)=m_Av_(fA) \\ v_(fA)=(p_f-m_Bv_(Bf))/(m_A) \end{gathered}`

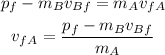
Then, we can replace the values to get:

`\begin{gathered} p_f=66kg\text{ m/s} \\ m_A=10kg \\ m_B=8kg_{} \\ v_(Bf)=4m/s \\ v_(fA)=\frac{66kg\text{ m/s - (8}kg)(4m/s)}{10kg} \\ v_(fA)=\frac{66kg\text{ m/s - 32 }kg\text{ m/s}}{10kg} \\ v_(fA)=\frac{34kg\text{ m/s}}{10kg} \\ v_(fA)=3.4m/s \end{gathered}`

Therefore, the final velocity of object A is 3.4 m/s