Question

The fox population in a certain region has a continuous growth rate of 5 percent per year. It is estimated that the population in the year 2000 was 12600. O for 2000). (a) Find a function that models the population t years after 2000 (t Hint: Use an exponential function with base e. Your answer is P(t) (b) Use the function from part (a) to estimate the fox population in the year 2008. Your answer is (the answer must be an integer)

Answer 1

The form of continuous growth is

`f\mleft(t\mright)=ae^(rt)`

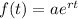
a is the initial amount

r is the rate of increase in decimal

Since the population in the year 2000 is 12600, then

`a=12600`

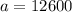
Since the growth rate is 5%, then

`r=(5)/(100)=0.05`

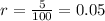
a)

Substitute the values of a and r in the form of the equation above to get the continuous growth equation of the population since the year 2000

`P\left(t\right)=12600e^(0.05t)`

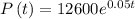
b)

Since we need the population in the year 2008, then

Subtract 2000 from 2008 to find the number of years t

`t=2008-2000=8`

Substitute t in the equation by 8

`\begin{gathered} P\left(8\right)=12600e^(0.05\left(8\right)) \\ P\left(8\right)=18796.99119 \end{gathered}`

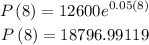
Round it to the whole number, then

P(8) = 18797

There were about 18797 foxes in 2008