Question

Solve the following systems oy grapning, substitution
y=-(1)/(2)x-1
y=(1)/(4)x-4

Answer 1

The solution to the system of equations
`\(y = -(1)/(2)x - 1\) and \(y = (1)/(4)x - 4\)` is
`\(x = -4\)` and
`\(y = -1\).`

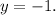
Step-by-step explanation:

To solve this system of equations, we can set the expressions for
`\(y\)` equal to each other:

`\[-(1)/(2)x - 1 = (1)/(4)x - 4.\]`

First, we can simplify the equation by multiplying both sides by 4 to get rid of the fraction:

`\[-2x - 4 = x - 16.\]`

Next, we can combine like terms by adding
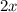`\(2x\)` to both sides:

`\[-4 = 3x - 16.\]`

Now, add 16 to both sides to isolate
`\(3x\)`:

`\[12 = 3x.\]`

Finally, divide both sides by 3 to solve for
`\(x\)`:

`\[x = -4.\]`

Now that we know
`\(x\)`, we can substitute this value back into one of the original equations to find
`\(y\)`. Using the first equation
`\(y = -(1)/(2)x - 1\)`, substitute
`\(x = -4\)`:

`\[y = -(1)/(2)(-4) - 1 = 2 - 1 = 1.\]`

Therefore, the solution to the system is
`\(x = -4\)` and
`\(y = -1\)`.