Question

Use it in a lot of the time it can

Answer 1

Part A. We are asked to determine the derivative of each of the functions. To do that we will use the chain rule:

`(d)/(dx)f(g(x))=f^(\prime)(g(x))g^(\prime)(x)`

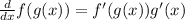
This means that we take the derivative of the function as a whole and then we multiply it by the derivative of the function inside the parenthesis.

Let's take Alice's function.

`f(x)=15(4+3x)^4`

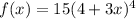
We have the following:

`\begin{gathered} f(x)=15(g(x))^4 \\ g(x)=4+3x \end{gathered}`

Taking the derivative of f(x) we get:

`f^(\prime)(x)=60(g(x))^3g^(\prime)(x)`

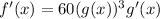
Now, we take the derivative of g(x):

`g^(\prime)(x)=3`

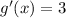
Now, we substitute the values:

`\begin{gathered} f^(\prime)(x)=60(4+3x)^3(3) \\ \\ f^(\prime)(x)=180(4+3x)^3 \end{gathered}`

And thus we get the derivative of the function.

The same procedure is done for the other functions.

Part B.

Let's take the function for Dani's guess:

`f(x)=(1)/(18)(4+3x)^6`

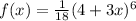
Applying the chain rule we get:

`f^(\prime)(x)=(6)/(18)(4+3x)^5(3)`

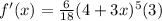
Simplifying we get:

`\begin{gathered} f^(\prime)(x)=(18)/(18)(4+3x)^5 \\ \\ f^(\prime)(x)=(4+3x)^5 \end{gathered}`

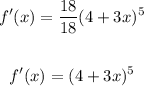
Therefore, Dani was the student that was correct.