Question

What two numbers multiple to 160, and add up to -4?

Answer 1

Let X be one number and Y be other number. Then, we can write

`X\cdot Y=160`

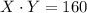
and

`X-Y=-4`

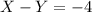
By moving -Y to the right hand side, we get

`X=Y-4`

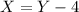
By substituting the last expression into the first one, we get

`(Y-4)\cdot Y=160`

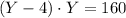
which gives

`\begin{gathered} Y^2-4Y=160 \\ Y^2-4Y-160=0 \end{gathered}`

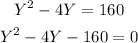
So, we have a quadratic function, which we can solve by means of the quadractic formula:

`Y=\frac{-(-4)\pm\sqrt[]{(-4)^2-4(1)(-160})}{2}`

which gives

`\begin{gathered} Y=\frac{4\pm\sqrt[]{16+640}}{2} \\ Y=(4\pm25.6)/(2) \end{gathered}`

So, we have 2 solutions:

`\begin{gathered} Y=(29.6)/(2)=14.8 \\ \text{and} \\ Y=(-21.6)/(2)=-10.8 \end{gathered}`

By substituting the fist solution into our first equation, we get

`\begin{gathered} X\cdot(14.81)=160 \\ X=(160)/(14.8) \\ X=10.81 \end{gathered}`

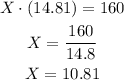
Now, by substituting the second solution into our first equation, we h ave

`\begin{gathered} X\cdot(-10.8)=160 \\ X=(160)/(-10.8) \\ X=-14.81 \end{gathered}`

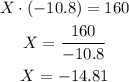
Lets check one solution. For X=10.81 and Y=14.81 we have

`\begin{gathered} (10.81)(14.8)\approx160 \\ \text{and} \\ 110.81-14.8\approx-4 \end{gathered}`

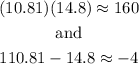
Now, lets chech the second solution. For X=-14.81 and Y=-10.81 we have

`\begin{gathered} (-10.81)(-14.8)\approx160 \\ \text{and} \\ -14.81+10.81\approx-4 \end{gathered}`

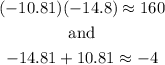
They are correct !! So, one solution is X=10.81 and Y=14.8 and the other solution is X=-14.81 and Y=-10.81.