Question

What is the nature of roots and the discriminant? The question has been answered but it differs from my option choice! The answer calculated by the previous instructor was discriminant: -108 and no real roots

Answer 1

Step-by-step explanation

Here, we want to get the discriminant and the nature of the roots

To get the discriminant, we write the equation in the standard form by expanding the given one

We have this as:

`\begin{gathered} y=-3(x+2)^2 \\ y=-3(x^2+4x+4)=-3x^2-12x-12 \end{gathered}`

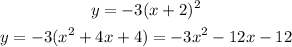
The formula for finding a discriminant is:

`D=b^2-4ac`

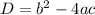
a is the coefficient of x^2 which is -3

b is the coefficient of x which is -12

c is the last number

Substituting these values. we have the discriminant as:

`D=-12^2-4(-3)(-12)\text{ = 144-144 = 0}`

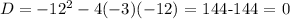
Whenever the discriminant is zero, what we have is a repeated real number solution