Question

The points (7, 3) and (7, 5) are both in the solution region of the inequality x – 2y < 3. Compute x – 2y for both of these points.Which point comes closest to satisfying the equation x – 2y = 3? That is, for which (x, y) pair is x – 2y closest to 3?

Answer 1

Part a.

In this case, we need to substitute the given point values into the expression x-2y. Then for point (7,3), we have

`\begin{gathered} 7-2(3) \\ \text{which gives} \\ 7-6=1 \end{gathered}`

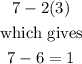
Now, for point (7,5) we have

`\begin{gathered} 7-2(5) \\ \text{which gives} \\ 7-10=-3 \end{gathered}`

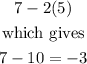
Part b.

As we can note, in the first case we got 1 which is 2 units from 3. In the second case, we got -3, which is 6 units from 3. Therefore, point (7,3) gives the closest value to 3