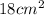1 Answer

Sameera Liyanage · Answer 1 · 2023-03-13T16:17:26+0000

First, calculate the surface area of each figure and then compare them.

Cube:

The cube is made up from 6 equal square surfaces. Then, the surface area is six time the area of one square. The area of each square is 9 squared cm, since:

$A=l^2=(3\operatorname{cm})^2=9cm^2$

Then, the surface area of the cube is:

$\begin{gathered} S=6\cdot9cm^2 \\ =54cm^2 \end{gathered}$

Rectangular prism

The rectangular prism has 6 faces, which are 3 pairs of rectangles.

Find the area of each type of rectangle. Then, add them twice to find the surface of the prism:

The first type of rectangle has sides of 3cm and 2cm. Then, the area is equal to:

$(3\operatorname{cm})(2\operatorname{cm})=6cm^2$

The second type of rectangle has sides of 3cm and 6cm. Then, the area is equal to:

$(3\operatorname{cm})(6\operatorname{cm})=18cm^2$

The third type of rectangle has sides of 2cm and 6cm. Then, the area is equal to:

$(2\operatorname{cm})(6\operatorname{cm})=12cm^2$

Then, the total surface area of the prism is:

$\begin{gathered} S=6cm^2+6cm^2+12cm^2+12cm^2+18cm^2+18cm^2 \\ =72cm^2 \end{gathered}$

Finally, substract the area of the cube from the area of the rectangular prism to find how much greater the area of the prism is:

Therefore, the answer is:

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions