Question

Graph the image of square EFGH after a rotation 90° counterclockwise around the origin.

Answer 1

Answer:

See the graph below

Step-by-step explanation:

Given:

Quadrilaterla EFGH on a coordinate plane

To find:

to graph the quadrilateral after a rotation of 90° counterclockwise around the origin.

The rule for a 90° counterclockwise around the origin is given as:

`\begin{gathered} (x,\text{ y\rparen}\rightarrow\text{ \lparen-y, x\rparen} \\ Switch\text{ x anf y and }negate\text{ the y while keeping x constant} \end{gathered}`

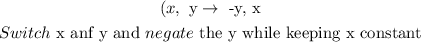
We will apply the rules to the coordinates of EFGH:

E = (3, 3)

F = (6, 3)

G = (6, 6)

H = (3, 6)

Applying the rule:

`\begin{gathered} (3,\text{ 3\rparen }\rightarrow\text{ \lparen3, 3\rparen }\rightarrow\text{ \lparen-3, 3\rparen} \\ E^(\prime)\text{ = \lparen-3, 3\rparen} \\ \\ (6,\text{ 3\rparen }\rightarrow(3,\text{ 6\rparen }\rightarrow(-3,\text{ 6\rparen} \\ F^(\prime)\text{ = \lparen-3, 6\rparen} \\ \\ (6,\text{ 6\rparen }\rightarrow\text{ \lparen6, 6\rparen }\rightarrow(-6,\text{ 6\rparen} \\ G^(\prime)\text{ = \lparen-6, 6\rparen} \\ \\ (3,\text{ 6\rparen }\rightarrow(6,\text{ 3\rparen }\rightarrow(-6,\text{ 3\rparen} \\ H^(\prime)\text{ = \lparen-6, 3\rparen} \end{gathered}`

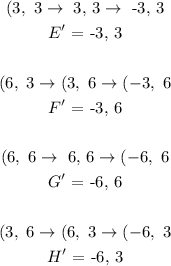
Plotting the graph: