1 Answer

Ask a Question

Bingerz · Answer 1 · 2023-05-17T11:49:29+0000

We know that

• The sphere diameter is 8.55 cm.

,

• The temperature change is from 30 C to 155 C.

First, we have to find the radius of the sphere. The radius is the half diameter.

$\begin{gathered} r=(d)/(2)=\frac{8.55\operatorname{cm}}{2} \\ r=4.275\operatorname{cm} \end{gathered}$

Now we have to find the volume of the sphere using the following formula.

$V=(4)/(3)\pi(r)^3$

Where r = 4.275 cm.

$\begin{gathered} V=(4)/(3)\pi(4.275\operatorname{cm})^3 \\ V\approx327.26(cm)^3 \end{gathered}$

Then, we use the following formula

Where the initial volume is 327.26 cubic cm, B is a constant about thermal expansion for aluminum, and we have to find the final volume to then calculate the percentage change.

$\begin{gathered} \Delta V=75*10^(-6)\cdot327.26(155-30) \\ \Delta V=75*10^(-6)\cdot327.26(125) \\ \Delta V\approx3.07(cm)^3 \end{gathered}$

This means that the volume change is 3.07 cubic centimeters.

At last, we have to divide the volume change by the initial volume, and then we have to multiply it by 100% to express it as a percentage.

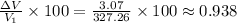
$(\Delta V)/(V_1)*100=(3.07)/(327.26)*100\approx0.938$

0 Comments

Your comment on this question:

Your answer

1 Answer

Therefore, the percentage change is 0.938%.

0 Comments

Your comment on this answer:

Other Questions