a. The formula relating y (the amount of the substance) to t (the time in minutes) can be expressed as:
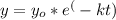
b. The amount of the substance present in 6 minutes is approximately 16.2 mg.
How much will be present in minutes?
(a) The formula relating y (the amount of the substance) to t (the time in minutes) can be expressed as:
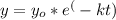
Where:
y₀ is the initial amount of the substance (27.1 mg in this case),
k is the decay constant (related to the half-life), and
t is the time in minutes.
To determine the value of k, use the relationship between the half-life (T½) and the decay constant (k):
T½ = ln(2) / k
Given that the half-life is 8 minutes, substitute this value into the equation and solve for k:
8 = ln(2) / k
Solving for k:
k = ln(2) / 8
Now substitute the values of y₀ and k back into the formula:
y = 27.1 *
 / 8) * t)
/ 8) * t)
(b) To find how much of the substance will be present in 6 minutes, substitute t = 6 into the formula:
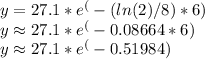
y ≈ 27.1 * 0.5959
y ≈ 16.18
By rounding to the nearest tenth, the amount of the substance present in 6 minutes is approximately 16.2 mg.
Complete question
A sample of a radioactive substance has an initial mass of 27.1 mg. This substance follows a continuous exponential decay model and has a half-life of 8 minutes. (a) Lett be the time in minutes) since the start of the experiment, and let y be the amount of the substance at time t. . Dino ? Write a formula relating y to t. Use exact expressions to fill in the missing parts of the formula. Do not use approximations. y = ---e^---t (b) How much will be present in 6 minutes? Do not round any intermediate computations, and round your answer to the nearest tenth.