Answer:
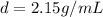
Step-by-step explanation:
Hello there!
In this case, since the density of the metal is computed as shown below:
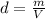
We need to calculate the volume of the solid by subtracting the final volume and the initial volume of water:
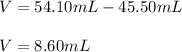
Thus, we obtain:
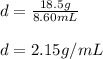
Best regards!