Question

part A: A very flexible helium-filled balloon is released from the ground into the air at 20. ∘C . The initial volume of the balloon is 5.00 L , and the pressure is 760. mmHg . The balloon ascends to an altitude of 20 km , where the pressure is 76.0 mmHg and the temperature is − 50. ∘C . What is the new volume, V2 , of the balloon in liters, assuming it doesn't break or leak?part B: Consider 4.60 L of a gas at 365 mmHg and 20. ∘C . If the container is compressed to 3.00 L and the temperature is increased to 33 ∘C , what is the new pressure, P2 , inside the container? Assume no change in the amount of gas inside the cylinder.

Answer 1

The volume of the gas is V2 is 38.1 liters

Step-by-step explanation

Given that;

`\begin{gathered} \text{ The initial temperature of the balloon is 20}\degree C \\ \text{ The initial volume of the balloon is 5.0L} \\ \text{ The initial pressure of the balloon is 760 mmHg} \\ \text{ The final temperature of the balloon is - 50}\degree C \\ \text{ The final pressure of the balloon is 76 mmHg} \end{gathered}`

To find the final volume of the balloon, follow the steps below

Step 1; Write the general gas law equation

`\text{ }\frac{P1\text{ }*\text{ V1}}{T1}\text{ }=\text{ }\frac{\text{ P2}*\text{ V2}}{T2}`

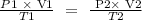
Step 2; Convert the temperature to kelvin

`\begin{gathered} \text{ t1 }=\text{ 20}\degree C \\ \text{ T }=\text{ t }+\text{ 273.15} \\ \text{ T }=\text{ 20 + 273.15} \\ \text{ T = 293.15K} \\ \\ t2\text{ }=\text{ -50}\degree C \\ \text{ T = -50 + 273.15} \\ \text{ T}=\text{ 223.15K} \end{gathered}`

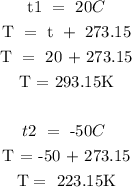
Step 3; Substitute the given that into the formula given

`\begin{gathered} \text{ }(760*5)/(293.15)\text{ }=\text{ }\frac{76\text{ }*\text{ V2}}{223.15} \\ \text{ cross multiply} \\ \text{ 760 }*\text{ 5}*\text{ 223.15 }=\text{ 76 }*\text{ v2}*\text{ 293.15} \\ \text{ 847970 }=\text{ 22, 279.4 }*\text{ v2} \\ \text{ divide both sides by 22294} \\ \text{ }(8479890)/(222794)=\text{ }\frac{22294\text{ V2}}{22294} \\ \text{ v2 }=\text{ 38.1 Liters} \end{gathered}`

Hence, the volume of the gas is V2 is 38.1 liters