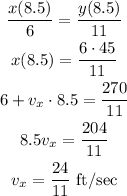A woman 6 ft tall walks away from a 17 ft tall pole with a street light on top of it.
Graphically:
From the diagram, we can say that:
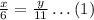
The laws of motion of the woman and the shadow with respect to the base of the pole are:
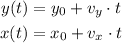
Where x0 and y0 are the initial positions, vx and vy are the shadow speed and the speed of the woman, respectively. We know that vy = 4 ft/s, so if we say that the starting point for the woman was 11 feet away from the pole, then using equation (1):

Then, the laws of motion are:
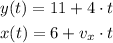
We now calculate the instant of time when y = 45 ft. Using the law of motion of the woman:
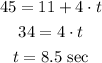
Again, using the equation (1):