Question

Hello, I am currently very stuck with this problem and I am unsure as to how I would solve it.

Answer 1

We have the equation

`20y=x^2-10-15`

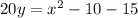
Let's complete the square, to do it let's add and subtract 25 on the right side

`\begin{gathered} 20y=x^2-10-15+25-25 \\ \\ 20y=(x-5)^2-15-25_{} \\ \\ 20y=(x-5)^2-40 \\ \\ \end{gathered}`

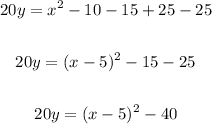
Now we can have y in function of x

`\begin{gathered} y=(1)/(20)(x-5)^2-2 \\ \\ \end{gathered}`

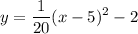
Now we can already identify the vertex because it's in the vertex form:

`y=a(x-h)+k`

Where the vertex is

`(h,k)`

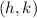
As we can see, h = 5 and k = -2, then the vertex is

`(5,-2)`

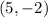
Now we can continue and find the focus, the focus is

`\mleft(h,k+(1)/(4a)\mright)`

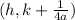
We have a = 1/20, therefore

`\begin{gathered} \mleft(5,-2+5\mright) \\ \\ (5,3) \end{gathered}`

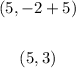
The focus is

`(5,3)`

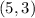
And the last one, the directrix, it's

`y=k-(1)/(4a)`

Then

`\begin{gathered} y=-2-5 \\ \\ y=-7 \end{gathered}`

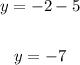
Hence the correct answer is: vertex (5, -2); focus (5, 3); directrix y = -7