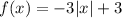Question

2. Write the equation of the graph shown below. 3 1 -2 0 2 1-

Answer 1

The function in the graph is V shaped, this indicates that it corresponds to a function of an absolute value of x:

`f(x)=|x|`

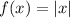
The V opens downwards, which means that the coefficient that multiplies the module (a) is negative:

`f(x)=-|x|`

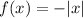
→ This means rthat when we calculate the value of "a", this value has to be negative

As you can see in the graph, the vertex of the function is (0,3)

Following the vertex form:

`f(x)=a|x-x_v|+y_v`

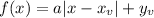
Where xv represents the x-coordinate of the vertex and yv represents the y-coordinate of the vertex. Replace them in the formula and we get that:

`\begin{gathered} f(x)=a|x-0|+3 \\ f(x)=a|x|+3 \end{gathered}`

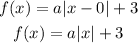
Now all we need to do is determine the value of "a", for this we have to use one point of the function and replace it in the formula, this way "a" will be the only unknown.

Lets take for example one of the roots (points where the function crosses the x-axis)

Point (1, 0)→ replace it in the formula

`\begin{gathered} 0=a|1|+3 \\ 0=a+3 \\ a=-3 \end{gathered}`

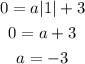
Now that we know the value of a, we can determine the wquation of the function as

`f(x)=-3|x|+3`