Question

The figure below shows a right triangle:

What is r ÷ p equal to? (6 points)

Group of answer choices

A. sin y°

B. sin x°

C. tan y°

D. tan x°

Answer 1

tan y°

Explanation:

by using the Sine Rule (See attached), we can form the equation:

`(r)/(sin (y)) = (p)/(sin (x))`

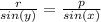
rearranging this, we get:

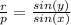`(r)/(p) =(sin(y))/(sin(x))` ---------------------eq 1

Recall that all internal angles of a triangle must sum to 180°. we observe that we have a right triangle where one of the angles is 90°. It then follows that the sum of the other two angles must sum to 90°

i.e x + y = 90°

with a little rearranging, we get

x = (90° - y)

Substituting this into eq 1 above, we get:

`(r)/(p) =(sin(y))/(sin(90- y))` ---------eq 2

recall that from the trigonometric co-function identities,

sin (90°- y) = cos y

substituting this into eq 2 gives :

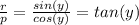`(r)/(p) =(sin(y))/(cos(y)) = tan(y)` (answer)