Question

The ratio between the radius of the base and the height of a cylinder is 2:3. If it's volume is 1617cm^3, find the total surface area of the cylinder.

Answer 1

The ratio of the radius to the height of the cylinder is

`2\colon3`

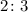
Let the radius be

`r=2x`

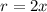
Let the height be

`h=3x`

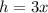
The volume of the cylinder is given below as

`V=1617cm^3`

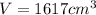
Concept:

The volume of a cylinder is given below as

`V_{\text{cylinder}}=\pi* r^2* h`

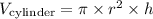
By substituting values, we will have

`\begin{gathered} V_{\text{cylinder}}=\pi* r^2* h \\ 1617=(22)/(7)*(2x)^2*(3x) \\ 1617=(22)/(7)*4x^2*3x \\ 1617*7=264x^3 \\ \text{divdie both sides by 264} \\ (264x^3)/(264)=(1617*7)/(264) \\ x^3=(343)/(8) \\ x=\sqrt[3]{(343)/(8)} \\ x=(7)/(2) \end{gathered}`

The radius therefore will be

`\begin{gathered} r=2x=2*(7)/(2) \\ r=7cm \end{gathered}`

The height of the cylinder will be

`\begin{gathered} h=3x=3*(7)/(2) \\ h=(21)/(2)cm \end{gathered}`

The formula for the total surface area of a cylinder is given below as

`T\mathrm{}S\mathrm{}A=2\pi r(r+h)`

By substituting the values, we will have

`\begin{gathered} TSA=2\pi r(r+h) \\ TSA=2*(22)/(7)*7(7+(21)/(2)) \\ TSA=44(7+(21)/(2)) \\ TSA=44*7+44*(21)/(2) \\ TSA=308+462 \\ TSA=770cm^2 \end{gathered}`

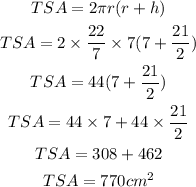
Hence,

The total surface area of the cylinder is = 770cm²