Question

Find the lengths of the diagonals of rectangle WXY Z where WY-2x + 34 and XZ = 3x – 26The length of each diagonal isunits.

Answer 1

To solve the exercise, you can first draw a picture to better understand the statement. So,

Now, in a rectangle, the lengths of the diagonals measure the same. So,

`\begin{gathered} WY=XZ \\ -2x+34=3x-26 \end{gathered}`

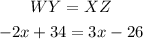
To solve for x first subtract 34 from both sides of the equation

`\begin{gathered} -2x+34-34=3x-26-34 \\ -2x=3x-60 \end{gathered}`

Subtract 3x from both sides of the equation

`\begin{gathered} -2x-3x=3x-60-3x \\ -5x=-60 \end{gathered}`

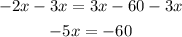
Divide by -5 into both sides of the equation

`\begin{gathered} (-5x)/(-5)=(-60)/(-5) \\ x=12 \end{gathered}`

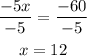
Finally, replace the value of x in the length of any of the diagonals, for example, the diagonal WY

`\begin{gathered} WY=-2x+34 \\ WY=-2(12)+34 \\ WY=-24+34 \\ WY=10 \end{gathered}`

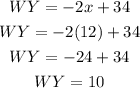
Therefore, the length of each diagonal is 10 units.