Final Answer:
a)
 is the resultant force when forces
is the resultant force when forces
 and
and
 are combined, calculated using vector addition.
are combined, calculated using vector addition.
Step-by-step explanation:
The resultant force
 is determined by vector addition, where the magnitudes and directions of \( F_1 \) and
is determined by vector addition, where the magnitudes and directions of \( F_1 \) and
 are considered. The formula for vector addition is
are considered. The formula for vector addition is
 , where
, where
 are the x-components of
are the x-components of
 and
and
 respectively, and
respectively, and
 and
and
 are the y-components. This yields the magnitude of
are the y-components. This yields the magnitude of
 .
.
To find the direction, the angle
 can be calculated using
can be calculated using
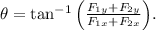
b)
 is the vector sum of
is the vector sum of
 and
and
 , calculated by adding their respective x and y components.
, calculated by adding their respective x and y components.
c)
 is the vector difference between
is the vector difference between
 and
and
 , obtained by subtracting their x and y components.
, obtained by subtracting their x and y components.
d)
 is the reverse vector difference, obtained by subtracting
is the reverse vector difference, obtained by subtracting
 's components from
's components from
 's.
's.
In summary, vector addition and subtraction involve combining or separating forces along the x and y axes, and the resulting vectors provide the magnitude and direction of the net force. These principles are fundamental in physics for analyzing and understanding the motion of particles under the influence of multiple forces.