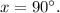Main Answer:
a. Solve the initial value problem for the differential equation
 with the initial condition ( y(0) = 2 ).
with the initial condition ( y(0) = 2 ).
b. Solve the equation ( 2x + 5y = 10 ) for ( y ).
c. Find the general solution of
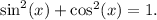
d. Determine the value of ( x ) in the right-angled triangle with sides ( a = 3 ), ( b = 4 ), and ( c = 5 \).
Step-by-step explanation:
a. Calculus:
The given differential equation is
 To solve this, integrate both sides with respect to ( x ):
To solve this, integrate both sides with respect to ( x ):
![\[ \int{dy} = \int{3x^2 dx} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7dfpfsmoucgpiki8mp5kl2ziao2q183831.png)
Integrating, we get:
![\[ y = x^3 + C \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cvhyzbyoy01e63dgbcs2o2g1vpctgdubpg.png)
Now, apply the initial condition \( y(0) = 2 \) to find the constant \( C \):
![\[ 2 = 0^3 + C \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ks2m4danysmjm4cbru4l8vjmcf7e4thbjc.png)
Therefore, \( C = 2 \), and the solution to the initial value problem is \( y = x^3 + 2 \).
---
b. Algebra:
*
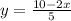
To solve the equation ( 2x + 5y = 10 ) for y , isolate y on one side:
\[ 5y = 10 - 2x \]
Divide both sides by 5:
![\[ y = (10 - 2x)/(5) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4hqtotfzmvwpl8z5b0s0k6ddbkhtftpp6k.png)
So, the solution is
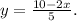
---
c. Trigonometry:
The given equation
 is a fundamental trigonometric identity known as the Pythagorean identity. It holds true for all values of \( x \) and is a foundational result in trigonometry. The identity states that the square of the sine of an angle plus the square of the cosine of the same angle is always equal to 1.
is a fundamental trigonometric identity known as the Pythagorean identity. It holds true for all values of \( x \) and is a foundational result in trigonometry. The identity states that the square of the sine of an angle plus the square of the cosine of the same angle is always equal to 1.
---
d. Geometry:
In a right-angled triangle with sides ( a = 3 ), \( b = 4 \), and \( c = 5 \) (following the Pythagorean theorem
 the angle x opposite the side \( a \) is the angle
the angle x opposite the side \( a \) is the angle
 This is because the sides satisfy the conditions for a Pythagorean triple, where the square of the hypotenuse (\( c \)) is equal to the sum of the squares of the other two sides a and b . Therefore,
This is because the sides satisfy the conditions for a Pythagorean triple, where the square of the hypotenuse (\( c \)) is equal to the sum of the squares of the other two sides a and b . Therefore,