Final Answer:
![\[f(x) = \sum_(n=0)^(\infty) nx^n.\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/h335k8ql2naasamfa3rnsywih2s9jpmuv6.png)
The power series representation of
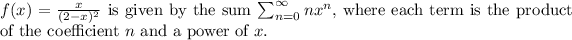
Step-by-step explanation:
The given function
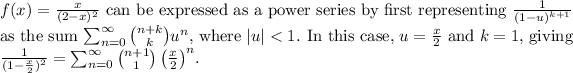
Multiplying both sides by
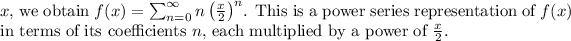
The resulting series is a representation of
 as an analytical function, particularly useful for various mathematical analyses and computations.
as an analytical function, particularly useful for various mathematical analyses and computations.