Question

Exercise 3.7.1: Proving statements about odd and even integers with direct proofs. info About Each statement below involves odd and even integers. An odd integer is an integer that can be expressed as 2k 1, where k is an integer. An even integer is an integer that can be expressed as 2k, where k is an integer.

Answer 1

The question is incomplete. The complete question is :

Each statement below involves odd and even integers. An odd integer is an integer that can be expressed as 2k+1, where k is an integer. An even integer is an integer that can be expressed as 2k, where k is an integer. Prove each of the following statements using a direct proof. (a) The sum of an odd and an even integer is odd. (b) The product of two odd integers is an odd integer.

Solution :

Odd number integers = 2k + 1, where k is integer

Even number integer = 2k

a). Odd integer + even integer

= 2k + 1 + 2k

= 4k + 1

= 2(2k) + 1

Let 2k = t, where t is integer

= 2t + 1

= Odd integer by definition

If number is 2t + 1 where t belongs to integer, then it is odd integer.

Hence proved.

b). Product of two odd integers :
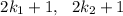`$2k_1 + 1,\ \ 2k_2 +1 $` where
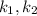`$k_1, k_2 $` belongs to integer.

`$(2k_1+1)(2k_2+1)= 4k_1k_2+2k_1+2k_2+1$`

`$2(2k_1k_2)+2(k_1+k_2)+1$`

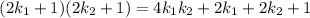
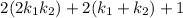
Let
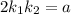`$2k_1k_2 = a$` and
`$k_1+k_2 = b $`

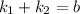
here, a and b belongs to integers since
`$k_1$` and
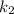`$k_2$` are integers.

We get:

2a+2b+1

= 2(a+b)+1

= 2l + 1, Let (a+b)=l and l belongs to integers.

It is odd integer by definition.

Hence proved.