Question

X^2- 20x = -2x – 80In (x+a)^2=b form please hurry

Answer 1

Completing Squares

It's given the following equation:

`x^2-20x=-2x-80`

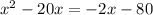
We are required to express the equation in the form:

`(x+a)^2=b`

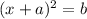
The first step is sending all the variables to the left side of the equation.

Adding 2x:

`\begin{gathered} x^2-20x+2x=-80 \\ \\ \text{Simplifying:} \\ x^2-18x=-80 \end{gathered}`

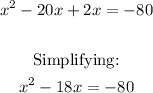
To complete squares, we need to recall the following identity:

`p^2+2pq+q^2=(p+q)^2`

The expression on the left side is missing the third term to be a perfect square. Note that comparing

p=x

2pq = -18x

This means that

q = -18x/2p

q = -18x/2x

q = -9

Now we know the value of the second term, we need to add q^2=81:

`x^2-18x+81=-80+81`

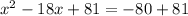
The left side of the equation is the square of x-9, and the right side can be calculated:

`(x-9)^2=1`

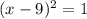
Now we have the required expression, where a=-9 and b = 1

-------------------