Question

Describe the transformations: F(x) = - 3(x +1)^2 + 5 What is the Parent Function: Opens UP or DOWN:Stretch or Shrink: Vertical Movement Up or Down, how many units:Horizontal Movement Left or Right, how many units:

Answer 1

You have the following transformation:

`F(x)=-3(x+1)^2+5`

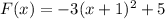
The previous function if a parabola. the Parent Function of any parabola is:

`y=x^2`

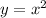
All others parabolas can be obtained by applying transformation to the Parent Function.

If you expand the parenthesis of F(x), you obtain:

`\begin{gathered} F(x)=-3(x^2+2x+1)+5=-3x^2-6x-3+5 \\ F(x)=-3x^2-6x+2 \end{gathered}`

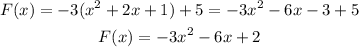
The dominant term, that is, the term with the variable x powered to 2, has a negative coefficient, it demands that the parabola open DOWN.

The coefficient of the dominant term is -3, then I-3I = 3 > 1. It means that the function stretches away from the x-axis.

The function streches way from x-axis by a factor of 3 units.

Vertical movement Up with 5 units. This is becasue the constant of the function, 5, which means the vertical translation of the Pater Function, if the constant is positive the translation is upward, if the translation is negative, it is downward.

Horizontal translation Left with 1 untit. The horizontal trasnlation is given by the constant term inside the quadratic parenthesis, in this case is + 1, whichi represents a translation of the graph to the left.