Question

F(x) = x^2 - 8x + 7Find the vertexaxis of symmetrygraph itfind the domainfind the range

Answer 1

Answers:

Vertex: (4, -9)

axis of symmetry: x = 4

Domain: (-∞, ∞)

Range: [-9, ∞)

Step-by-step explanation:

If we have a quadratic function with the form y = ax² + bx + c, the x-coordinate of the vertex will be at x = -b/2a

So, for f(x) = x² - 8x + 7, we get a = 1, b = -8 and c = 7, then the x-coordinate of the vertex will be:

`x=(-(-8))/(2(1))=(8)/(2)=4`

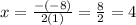
Then, the y-coordinate will be the value of f(x) when x = 4

`\begin{gathered} f(x)=x^2-8x+7 \\ f(4)=4^2-8(4)+7 \\ f(4)=16-32+7 \\ f(4)=-9 \end{gathered}`

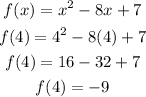
Therefore, the vertex of the equation is the point (x, y) = (4, -9).

The axis of symmetry is located in the vertex, since the parabola opens up, the axis of symmetry is the vertical line x = 4.

To graph the function, we need to find some points before and after the vertex. So, we will give values to x as 2, 3, 5, and 6. Then, we can calculate f(x) as:

`\begin{gathered} f(2)=2^2-8(2)+7=4-16+7=-5 \\ f(3)=3^2-8(3)+7=9-24+7=-8 \\ f(5)=5^2-8(5)+7=25-40+7=-8 \\ f(6)=6^2-8(6)+7=36-48+7=-5 \end{gathered}`

So, to graph the function, we will use the points (2, -5), (3, -8), (5, -8), (6, -5) and the vertex (4, -9). Therefore, the graph is:

Finally, the domain is the set of values that the variable x can take. In this case, x can be any number, so the domain is the set of all real numbers or written as an interval

(-∞, ∞)

And the range is the set of all values that f(x) can take. In this case, f(x) is always greater than -9, so the range is the set [-9, ∞)