Question

I don't understand how to do this problem. Could you explain to me how to do this problem? The formula for the perimeter of a rectangle is P=2l + 2w, where l is the length and w is the width. A rectangle has a perimeter of 24 inches. Find it's dimensions if it's length is 3 inches greater than it's width.

Answer 1

Given:

• Perimeter of the rectangle = 24 inches

,

• The length is 3 inches greater than it's width.

Let's find the dimensions of the rectangle.

To find the dimensions, apply the formula for perimeter of a rectangle:

P = 2l + 2w

Where l is the length and w is the width.

Given that the length is 3 inches greater than the width, the length can be expressed as:

l = (w + 3) inches

Substitute 24 for P and (w + 3) for l in the formula:

P = 2l + 2w

24 = 2(w + 3) + 2w

Let's solve the equation for w:

24 = 2(w + 3) + 2w

APply distributive property:

24 = 2(w) + 2(3) + 2w

24 = 2w + 6 + 2w

Combine like terms:

24 = 2w + 2w + 6

24 = 4w + 6

Subtract 6 from both sides:

24 -6 = 4w + 6 - 6

18 = 4w

Divide both sides by 4:

`\begin{gathered} (18)/(4)=(4w)/(4) \\ \\ 4.5=w \\ \\ w=4.5\text{ } \end{gathered}`

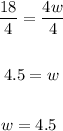
The width of the rectangle is 4.5 inches.

Since the lengh is 3 inches greater than the width, add 3 to 4.5 inches to get the length of the rectangle.

l = w + 3

l = 4.5 + 3

l = 7.5

The length of the rectangle is 7.5 inches.

Therefore, the dimensions of the rectangle are:

Length = 7.5 inches

Width = 4.5 inches

ANSWER:

Length = 7.5 inches

Width = 4.5 inches