Question

You have been given 3.152 g of copper from which you are to fashion a wire whose resistance is 2,473.562 ohms. The density of copper is 8900 kg/m 3 and the resistivity of copper is 1.7 x 10 -8 ohm m. What will the diameter, in mm, of the wire be that you fashion?

Answer 1

Given:

Mass of copper, m = 3.152 g = 0.003152 kg

Resistance = 2,473.562 ohms

Density of copper = 8900 kg/m³

Resistivity of copper = 1.7 x 10⁻⁸ ohm.m

Let's find the diameter of the wire.

Apply the density formula to find the volume:

`\begin{gathered} \rho=(m)/(v) \\ \\ v=(m)/(\rho)=(0.003152)/(8900) \\ \\ v=3.54*10^(-7)\text{ m}^3 \\ \\ (\pi r^2)l=3.54*10^(-7)\text{ m}^3 \end{gathered}`

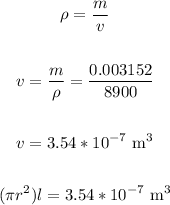
Now, apply the formula:

`\begin{gathered} R=(\rho l)/(A) \\ \\ l=(RA)/(\rho) \\ \\ l=(2473.562*\pi r^2)/(1.7*10^(-8)) \\ \\ (l)/(\pi r^2)=(2473.562)/(1.7*10^(-8)) \\ \\ (l)/(\pi r^2)=1.455*10^(11) \\ \\ l=1.455*10^(11)*\pi r^2 \end{gathered}`

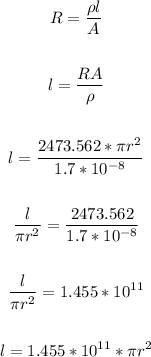
Now, combine both expressions for L:

`1.455*10^(11)*\pi r^2*\pi r^2=3.54*10^(-7)`

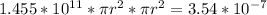
Solving further:

`\begin{gathered} (\pi r^2)^2=(3.54*10^(-7))/(1.455*10^(11)) \\ \\ (\pi r^2)=\sqrt{2.434*10^(-18)} \\ \\ \pi r^2=1.56*10^(-9) \\ \\ r^2=(1.56*10^(-9))/(\pi) \\ \\ r=\sqrt{(1.56*10^(-9))/(\pi)} \\ \\ r=2.228*10^(-5) \end{gathered}`

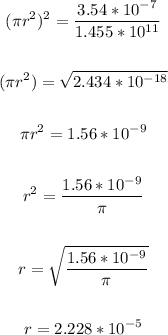
r is the radius.

We know that:

Diameter = 2 x radius

Thus, we have:

`\begin{gathered} d=(2.228*10^(-5))*2 \\ \\ d=4.4569*10^(-5)\text{ m} \\ \\ d=0.044569*10^(-3)m \\ \\ d=0.0446\text{ mm} \end{gathered}`

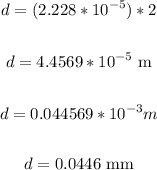
Therefore, the diameter in mm will be 0.0446 mm

ANSWER:

0.0446 mm