Step-by-step explanation:
We are given a zero-coupon bond that will be worth $10,000 if redeemed in 20 years time at an annual rate of 8% compounded;
(a) Daily
(b) Continuously
The formula for compounding annually is given as follows;
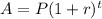
Here the variables are;

Note that this zero-coupon bond will yield an amount of $10,000 after 20 years at the rate of 8%. This means we already have;
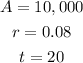
(a) For interest compounded daily, we would use the adjusted formula which is;
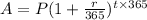
This assumes that there are 365 days in a year.
We now have;
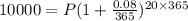

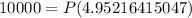
Now we divide both sides by 4.95216415047;
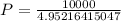
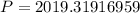
We can round this to 2 decimal places and we'll have;
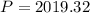
(b) For interest compounded continuously, we would use the special formula which is;

Note that the variable e is a mathematical constant whose value is approximately;
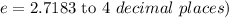
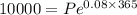
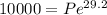
With the use of a calculator we have the following value;
