The formula for the half life is as follows:
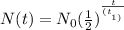
where N(t) is the final amount, N₀ is the initial amount, t is the time that passed, and t2 is the half-life.
The following are the given values in the problem:
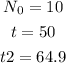
Substitute the values into the equation.
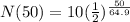
Simplify the right side of the equation. Divide 50 by 64.9 and then raise 1/2 by the obtained quotient. And finally, multiply the obtained value by 10.
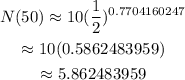
Therefore, after 50 days, it will become approximately 5.86 mg.