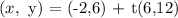We have the points:
p(0,-4) & q(3,2)
then, our directional vector will be:
pq(3,6)
now we have the equation of the line that we need to be parallel with:
(x,y)=(0,-4)+t(3,6)
We get (3,6) as follows:
we determine the directonal vector using the two point given:
p(0,-4) & q(3,2)
pq(3-0,2+4) =>pq=(3,6)
Now, the point of the line that is parallel to the one we got is: (-2,6):
Since a condition for being parallel is that the directional vector from one line is a product of the other, then:
(x,y) = (-2,6) + t(6,12)
As can be seen, the directional vector is parallel to the one found before (one is multiple of the other)
As for before, the equation of the line that passes by the point (-2,6) and is parallel to the line (x,y) = (0,-4) + t(3,6) is: