Question

In a housing project there are 180 households in which English is usually spoken, 80 in which Spanish is usually spoken, and 40 in which the language is other than English or Spanish. A researcher approaches a house at random to conduct an interview. What is the chance that the usual language in that household will NOT be English

Answer 1

The chance that the usual language in that household will NOT be English = 0.4

Explanation:

As given ,

Total households in which languages spoken is English = 180

Total households in which languages spoken is Spanish = 80

Total households in which languages spoken is other than English or Spanish = 40

So,

Total households = 180 + 80 + 40 = 300

Now,

Household in which English language is not spoken = 80 + 40 = 120

So,

The chances that the usual language in that household will NOT be English =
`(120)/(300) = (12)/(30) = (4)/(10) = 0.4`

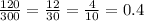
∴ we get

The chance that the usual language in that household will NOT be English = 0.4