Question

2? + kI - 20limI-5I - 5Solve for k to make it exist?

Answer 1

k = -1

Explanation:

The limit will exist if:

One of the roots of the equation in the numerator is 5. This happens because if this happens, we can simplify with the denominator. So

Solving a quadratic equation:

In the following format:

ax² + bx + c = 0

The solution is given by:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

In this question:

x² + kx - 20 = 0

The solution is:

`x=\frac{-k\pm\sqrt[]{k^2-4\ast1\ast(-20)}}{2}=\frac{-k\pm\sqrt[]{k^2-80}}{2}`

Since we want x = 5.

`\frac{-k+\sqrt[]{k^2+80}}{2}=5`
`-k+\sqrt[]{k^2-80}=10`
`\sqrt[]{k^2+80}=10+k`
`(\sqrt[]{k^2+80})^2=(10+k)^2`
`k^2+80=100+20k+k^2`
`k^2+80-100-20k-k^2=0`
`-20-20k=0`
`20k=-20`
`k=(-20)/(20)=-1`

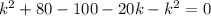
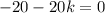
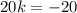
k = -1