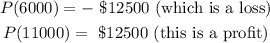Question

Hi, can you help me with this problem?A manufacturer has a monthly fixed cost of $42,500 and a production cost of $6 for each unit produced. The product sells for $11/unit.(a) What is the cost function?C(x)= (b) What is the revenue function?R(x)=(c) What is the profit function?P(x)= (d) Compute the profit (loss) corresponding to production levels of 6,000 and 11,000 units.P(6,000)=P(11,000)=

Answer 1

Given:

Fixed cost = b = $ 42,500

Production cost (Variable cost) /unit = m = $ 6/ unit

Let 'x' represent the number of unit, therefore the variable cost will be

`6x`

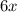
a) The cost function will be the sum of the fixed cost and the variable cost.

`C(x)=6x+42500`

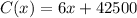
b) The revenue function is the amount the product is sold per unit.

Recall: 'x' represents the number of units.

Therefore,

`11* x=11x`

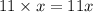
Hence, the revenue function R(x) is

`R(x)=11x`

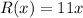
c) The profit function is the difference between the revenue function and the cost function.

`P\mleft(x\mright)=11x-\mleft(425000+6x\mright)=5x-42500`

Hence, the profit function is

`P\mleft(x\mright)=5x-42500`

d) Let us compute the profit (loss) values when the units are 6000 and 11000

Using the profit function

`P(x)=5x-42500`

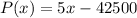
Therefore,

`\begin{gathered} P(6000)=5(6000)-42500=30000-42500=-\text{ \$12500} \\ P(11000)=5(11000)-42500=55000-42500=\text{ \$12500} \end{gathered}`

Hence,

`\begin{gathered} P(6000)=-\text{ \$12500 (which is a loss)} \\ P(11000)=\text{ \$12500 (this is a profit)} \end{gathered}`