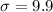Question

A sample was done , collecting the data below. Calculate the standard deviation,to one decimal place

Answer 1

....................................

Answer 2

By definition, the standard deviation is

`\sigma = \sqrt{\frac{\sum_(i=1)^(n)\left(x_i-\bar{x}\right)^2}{n}}`

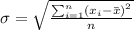
It seems hard so let's do it step by step, first, let's find the mean of the data

`\begin{gathered} \bar{x}=(24+29+2+21+9)/(5) \\ \\ \bar{x}=17 \end{gathered}`

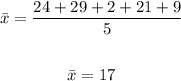
Now we have the mean value, let's do each value of the set minus the mean value

`\begin{gathered} x_1-\bar{x}=24-17=7 \\ \\ x_2-\bar{x}=29-17=12 \\ \\ x_3-\bar{x}=2-17=-15 \\ \\ x_4-\bar{x}=29-17=4 \\ \\ x_4-\bar{x}=9-17=-8 \end{gathered}`

Now we have the difference between each element and the mean value, let's do the square of all values

`\begin{gathered} (x_1-\bar{x})^2=7^2=49 \\ \\ (x_2-\bar{x})^2=12^2=144 \\ \\ (x_3-\bar{x})^2=(-15)^2=225 \\ \\ (x_4-\bar{x})^2=4^2=16 \\ \\ (x_5-\bar{x})^2=(-8)^2=64 \end{gathered}`

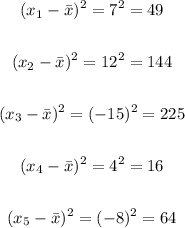
Now we have the square of the difference we sum them

`\begin{gathered} \sum_(i=1)^5\left(x_i-\bar{x}\right)^2=\left(x_1-\bar{x}\right)^2+\left(x_2-\bar{x}\right)^2+\left(x_3-\bar{x}\right)^2+\left(x_4-\bar{x}\right)^2+\left(x_5-\bar{x}\right)^2 \\ \\ \sum_(i=1)^5\left(x_i-\bar{x}\right)^2=49+144+225+16+64 \\ \\ \sum_(i=1)^5\left(x_i-\bar{x}\right)^2=498 \end{gathered}`

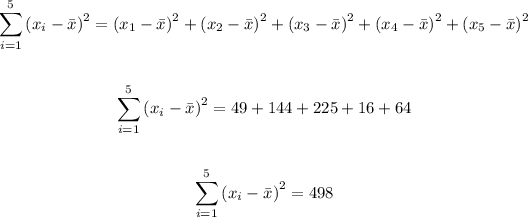
Now we have the sum we must divide by the number of elements, in that case, 5 elements

`\frac{\sum_(i=1)^5\left(x_i-\bar{x}\right)^2}{5}=99.6`

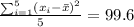
Now we take the square root of that value to have the standard deviation!

`\sigma=√(99.6)=9.979`

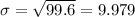
We write it using only one decimal the result would be

`\sigma=9.9`

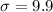
With no rounding.

Final answer:

`\sigma=9.9`